Birational geometry of moduli spaces and special varieties

Abstract:
The fundamental objects of study in algebraic geometry are the sets of solutions of systems of homogeneous polynomials. Algebraic geometry plays a central role in modern mathematics and has various conceptual connections with different areas such as complex analysis, topology and number theory.
Birational geometry is a part of algebraic geometry that deals with the geometry of an algebraic variety that depends only on its function field. The birational geometry of algebraic surfaces was widely studied in the years 1890-1910 by the Italian school with fundamental contributions by G. Castelnuovo, F. Enriques and F. Severi. From approximately 1970 to 1990 great breakthroughs were made by S. Mori, who gave a good theory for the birational geometry of 3-folds. In 2008 other great advances were made by C. Birkar, P. Cascini, C. D. Hacon, and J. McKernan in higher dimension [7].
Mori Dream Spaces, introduced by Y. Hu and S. Keel in 2000 [25], are a class of algebraic varieties that behave very well from the point of view of Mori’s minimal model program. They can be algebraically characterized as varieties whose ring of coordinates (Cox ring) is finitely generated [9]. In addition to this algebraic characterization, there are several algebraic varieties characterized by positivity properties of the anti-canonical divisor, such as Fano varieties, which are Mori Dream Spaces. Our project is meant to encompass a number of topics in birational geometry.
The topics can be divided into the following families:
- birational geometry of hypersurfaces of low degree and quadric bundles over an arbitrary field;
- birational geometry of moduli spaces of curves and stable maps;
- Calabi-Yau pairs and applications to the study of special subgroups of the Cremona group of the projective space.
- Secant varieties, tensor decomposition problems and applications.
There are several interplays between these topics that for now we exemplify in the following diagram leaving their detailed explanation for later:
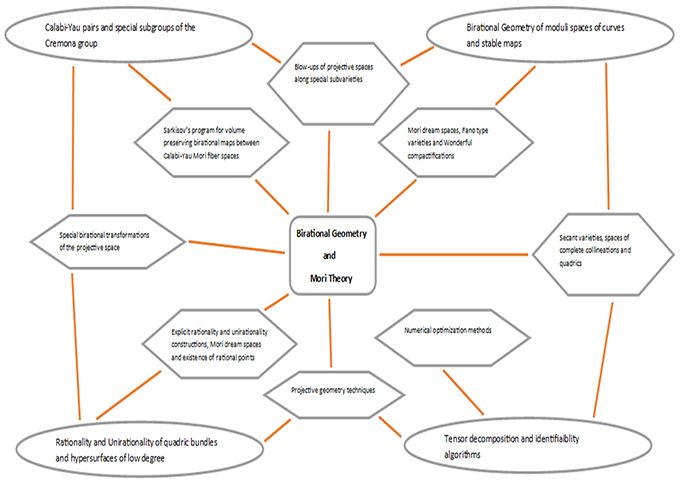
The ovals represent the main research topics while the hexagons include the main tools and methods we propose to investigate them.
The goal of the project is to obtain financial support for the continuation of the research in the topics listed above, as well as the production of algorithms and software packages. We plan to use the funding for:
- enhancing the collaboration among researchers in the group, by supporting their mobility and organizing meetings;
- support the participation of members of the group to meetings on the topic;
- organize two workshops in Italy for dissemination;
- invite international researchers in the field, for delivering advanced courses and for performing joint research with members of the group;
- support promising young researchers to continue their studies, in the theoretical and applicative aspects of our project, by providing them with post-doc positions and supporting their mobility.
Birational geometry is a part of algebraic geometry that deals with the geometry of an algebraic variety that depends only on its function field. The birational geometry of algebraic surfaces was widely studied in the years 1890-1910 by the Italian school with fundamental contributions by G. Castelnuovo, F. Enriques and F. Severi. From approximately 1970 to 1990 great breakthroughs were made by S. Mori, who gave a good theory for the birational geometry of 3-folds. In 2008 other great advances were made by C. Birkar, P. Cascini, C. D. Hacon, and J. McKernan in higher dimension [7].
Mori Dream Spaces, introduced by Y. Hu and S. Keel in 2000 [25], are a class of algebraic varieties that behave very well from the point of view of Mori’s minimal model program. They can be algebraically characterized as varieties whose ring of coordinates (Cox ring) is finitely generated [9]. In addition to this algebraic characterization, there are several algebraic varieties characterized by positivity properties of the anti-canonical divisor, such as Fano varieties, which are Mori Dream Spaces. Our project is meant to encompass a number of topics in birational geometry.
The topics can be divided into the following families:
- birational geometry of hypersurfaces of low degree and quadric bundles over an arbitrary field;
- birational geometry of moduli spaces of curves and stable maps;
- Calabi-Yau pairs and applications to the study of special subgroups of the Cremona group of the projective space.
- Secant varieties, tensor decomposition problems and applications.
There are several interplays between these topics that for now we exemplify in the following diagram leaving their detailed explanation for later:

The ovals represent the main research topics while the hexagons include the main tools and methods we propose to investigate them.
The goal of the project is to obtain financial support for the continuation of the research in the topics listed above, as well as the production of algorithms and software packages. We plan to use the funding for:
- enhancing the collaboration among researchers in the group, by supporting their mobility and organizing meetings;
- support the participation of members of the group to meetings on the topic;
- organize two workshops in Italy for dissemination;
- invite international researchers in the field, for delivering advanced courses and for performing joint research with members of the group;
- support promising young researchers to continue their studies, in the theoretical and applicative aspects of our project, by providing them with post-doc positions and supporting their mobility.
Dettagli progetto:
Referente scientifico: Massarenti Alex
Fonte di finanziamento: Bando PRIN 2022
Data di avvio: 28/09/2023
Data di fine: 28/09/2025
Contributo MUR: 62.000 €
Cofinanziamento UniFe: 11.625 €
Partner:
- Politecnico di FERRARA (capofila)
- Università degli Studi CATANIA
- Università degli Studi di TRENTO
